作者归档:beiyu
HarmonyOS使用动态属性设置实现跨文件样式设置
uniapp+vue3+ts签字上传
uniapp+vue3+ts微信小程序隐私协议组件
uniapp+vue3+uview-plus封装上传图片
echarts柱状图显示总数
uniapp+vue3+uview-plus登录界面
HarmonyOS第一课08:案例-应用内字体大小调节
HarmonyOS第一课08:用户首选项介绍
HarmonyOS第一课08:案例-首选项
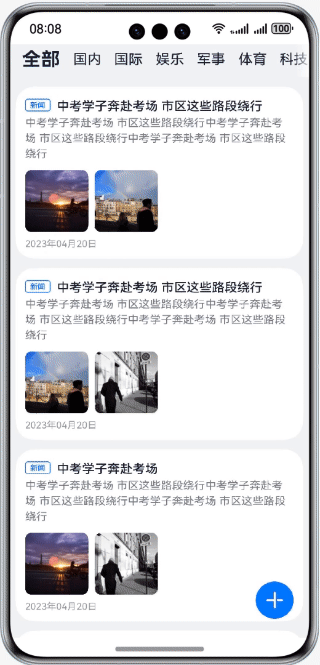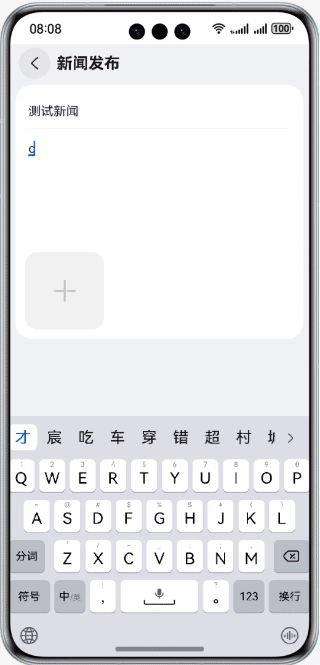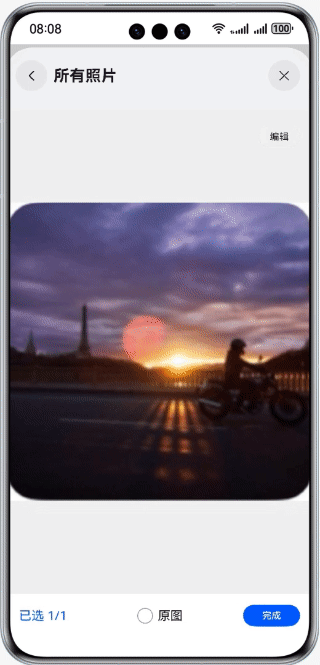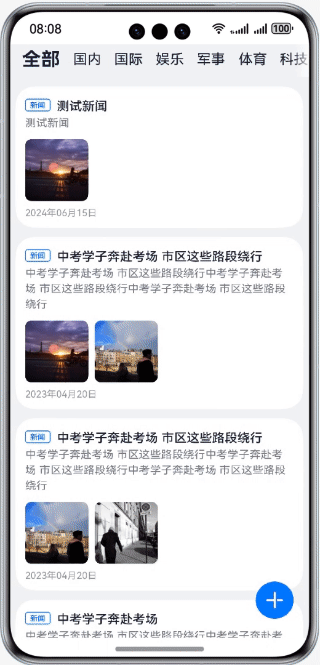
HarmonyOS第一课07:案例-新闻发布
效果演示
代码结构
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 |
├──entry/src/main/ets // 代码区 │ ├──common │ │ ├──constansts │ │ │ └──Constants.ets // 常量类 │ │ └──utils │ │ ├──FileUtil.ets // 文件工具类 │ │ ├──HttpUtil.ets // 网络请求 │ │ ├──Logger.ets // Logger公共类 │ │ └──ToastUtil.ets // Toast弹窗 │ ├──entryability │ │ └──EntryAbility.ets // 程序入口类 │ ├──pages │ │ ├──MainPage.ets // 新闻列表主页面 │ │ └──NewsEditPage.ets // 新闻发布页面 │ ├──view │ │ ├──FailureLayout.ets // 请求失败布局 │ │ ├──LoadingLayout.ets // 加载中布局 │ │ ├──LoadMoreLayout.ets // 加载更多布局 │ │ ├──NewsItem.ets // 新闻Item │ │ ├──NewsList.ets // 新闻列表 │ │ ├──NoMoreLayout.ets // 没有更多数据布局 │ │ ├──RefreshLayout.ets // 下拉刷新布局 │ │ └──UploadingLayout.ets // 上传中布局 │ └──viewmodel │ ├──GlobalContext.ets // 全局变量管理 │ ├──NewsData.ets // 新闻数据 │ ├──NewsTypeModel.ets // 新闻类型 │ ├──NewsTypeViewModel.ets // 新闻类型ViewModel │ ├──NewsViewModel.ets // 新闻列表ViewModel │ ├──RefreshListViewModel.ets // 刷新列表ViewModel │ ├──RefreshLoadingClass.ets // 刷新布局模型 │ └──ResponseResult.ets // 网络请求数据模型 ├──entry/src/main/resources // 资源文件 └──HttpServerOfNews // 服务端代码 |
启动服务
|
1 2 3 |
$ cd HttpServerOfNews $ npm install $ npm start |
代码
common
Constants.ets
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 |
export default class Constants { /** * The host address of the server. */ static readonly SERVER: string = 'http://192.168.10.37:9588'; /** * Get the news type. */ static readonly GET_NEWS_TYPE: string = 'news/getNewsType'; /** * Get the news list. */ static readonly GET_NEWS_LIST: string = 'news/getNewsList'; /** * Get the news list. */ static readonly UPLOAD_NEWS: string = 'news/addNews'; /** * Upload File */ static readonly UPLOAD_FILE: string = '/files/upload'; /** * UploadFile */ static readonly IMAGE_PREFIX: string = '/images/'; /** * url of NewsUploadPage */ static readonly NEWS_EDIT_PAGE: string = 'pages/NewsEditPage' /** * The request success status code. */ static readonly SERVER_CODE_SUCCESS: string = 'success'; /** * The off set coefficient. */ static readonly Y_OFF_SET_COEFFICIENT: number = 0.1; /** * The page size. */ static readonly PAGE_SIZE: number = 10; /** * The refresh and load height. */ static readonly CUSTOM_LAYOUT_HEIGHT: number = 70; /** * Gt tab data current page. */ static readonly GET_TAB_DATA_CURRENT_PAGE: number = 1; /** * Http request success status code. */ static readonly HTTP_CODE_200: number = 200; /** * The animation delay time. */ static readonly DELAY_ANIMATION_DURATION: number = 300; /** * The delay time. */ static readonly DELAY_TIME: number = 1000; /** * The animation duration. */ static readonly ANIMATION_DURATION: number = 2000; /** * The http timeout duration. */ static readonly HTTP_READ_TIMEOUT: number = 10000; /** * Content maxLine. */ static readonly CONTENT_MAX_LINE: number = 3; /** * List space. */ static readonly LIST_SPACE: number = 12; /** * Item img space. */ static readonly ITEM_IMG_SPACE: number = 8; /** * Type font weight. */ static readonly TYPE_FONT_WEIGHT: number = 700; /** * Title font weight. */ static readonly TITLE_FONT_WEIGHT: number = 500; /** * Desc font weight. */ static readonly DESC_FONT_WEIGHT: number = 400; /** * Type aspect ratio. */ static readonly TYPE_ASPECT_RATIO: number = 2; /** * Desc opacity. */ static readonly DESC_OPACITY: number = 0.6; /** * 100 percent. */ static readonly FULL_PERCENT: string = '100%'; /** * Divider width. */ static readonly DIVIDER_WIDTH: string = '90%'; /** * Release title. */ static readonly RELEASE_TITLE: string = '新闻发布'; } /** * The RefreshConstant constants. */ export const enum RefreshConstant { DELAY_PULL_DOWN_REFRESH = 50, CLOSE_PULL_DOWN_REFRESH_TIME = 150, DELAY_SHRINK_ANIMATION_TIME = 500 } /** * The refresh state enum. */ export const enum RefreshState { DropDown = 0, Release = 1, Refreshing = 2, Success = 3, Fail = 4 } /** * The newsList state enum. */ export const enum PageState { Loading = 0, Success = 1, Fail = 2 } /** * The file upload state enum. */ export const enum UploadingState { COMPLETE = 'complete', FAIL = 'fail' } /** * The request method enum. */ export const enum RequestMethod { POST = 'POST', GET = 'GET' } /** * The request content type enum. */ export const enum ContentType { JSON = 'application/json', FORM = 'multipart/form-data' } |
utils/FileUtil.ets
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 |
import { fileIo } from '@kit.CoreFileKit'; import { request } from '@kit.BasicServicesKit'; import { picker } from '@kit.CoreFileKit'; import Constants, { ContentType, RequestMethod, UploadingState } from '../constants/Constants'; import ResponseResult from '../../viewmodel/ResponseResult'; import Logger from './Logger'; import { showToast } from './ToastUtil'; /** * PhotoViewPicker * * @returns uri The uri for the selected file. */ export async function fileSelect(): Promise<string> { let photoSelectOptions = new picker.PhotoSelectOptions(); photoSelectOptions.MIMEType = picker.PhotoViewMIMETypes.IMAGE_TYPE; photoSelectOptions.maxSelectNumber = 1; let photoPicker = new picker.PhotoViewPicker(); try { let photoSelectResult = await photoPicker.select(photoSelectOptions); if (photoSelectResult && photoSelectResult.photoUris && photoSelectResult.photoUris.length > 0) { let imgUri = photoSelectResult.photoUris[0]; if (imgUri.indexOf('media/Photo')<0) { showToast($r('app.string.prompt_select_img')); return ''; } return photoSelectResult.photoUris[0]; } else { return ''; } } catch (err) { Logger.error('SelectedImage failed', JSON.stringify(err)); return ''; } } /** * Upload file. * * @param context Indicates the application BaseContext. * @param fileUri The local storage path of the file. * @returns the promise returned by the function. */ export function fileUpload(context: Context, fileUri: string): Promise<ResponseResult> { // Obtaining the Application File Path. let cacheDir = context.cacheDir; let imgName = fileUri.split('/').pop() + '.jpg'; let dstPath = cacheDir + '/' + imgName; let url: string = Constants.SERVER + Constants.UPLOAD_FILE; let uploadRequestOptions: request.UploadConfig = { url: url, header: { 'Content-Type': ContentType.FORM }, method: RequestMethod.POST, files: [{ filename: imgName, name: 'file', uri: 'internal://cache/' + imgName, type: 'jpg' }], data: [] }; let serverData = new ResponseResult(); return new Promise((resolve: Function, reject: Function) => { try { // Copy the URI to the cacheDir directory and upload the file. let srcFile = fileIo.openSync(fileUri); let dstFile = fileIo.openSync(dstPath, fileIo.OpenMode.READ_WRITE | fileIo.OpenMode.CREATE); fileIo.copyFileSync(srcFile.fd, dstFile.fd); fileIo.closeSync(srcFile); fileIo.closeSync(dstFile); // Upload the file. request.uploadFile(context, uploadRequestOptions).then((data: request.UploadTask) => { data.on(UploadingState.COMPLETE, (result: Array<request.TaskState>) => { Logger.info('uploadFile success', JSON.stringify(result)); if (result && result.length >= 1) { serverData.code = Constants.SERVER_CODE_SUCCESS; serverData.msg = result[0].message; serverData.data = Constants.IMAGE_PREFIX + result[0].path.split('/').pop(); resolve(serverData); } }); data.on(UploadingState.FAIL, (result: Array<request.TaskState>) => { Logger.info('uploadFile failed', JSON.stringify(result)); if (result && result.length >= 1) { serverData.msg = $r('app.string.upload_error_message'); reject(serverData); } }) }).catch((err: Error) => { Logger.error('uploadFile failed', JSON.stringify(err)); reject(serverData); }); } catch (err) { Logger.error('uploadFile failed', JSON.stringify(err)); reject(serverData); } }) } |
utils/HttpUtil.ets
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 |
import { http } from '@kit.NetworkKit'; import { NewsData } from '../../viewmodel/NewsData'; import ResponseResult from '../../viewmodel/ResponseResult'; import Constants, { ContentType } from '../constants/Constants'; /** * Initiate an HTTP GET request to the specified URL. * * @param url URL for initiating an HTTP request. */ export function httpRequestGet(url: string) { return httpRequest(url, http.RequestMethod.GET); } /** * Initiate an HTTP POST request to the specified URL. * * @param url URL for initiating an HTTP request * @param newsData Additional data of the request * @returns */ export function httpRequestPost(url: string, newsData: NewsData) { return httpRequest(url, http.RequestMethod.POST, newsData); } /** * Initiates an HTTP request to a given URL. * * @param url URL for initiating an HTTP request * @param method Request method. * @param extraData Additional data of the request. * @returns Returns {@link ResponseResult}. */ function httpRequest(url: string, method: http.RequestMethod, params?: NewsData): Promise<ResponseResult> { let httpRequest = http.createHttp(); let responseResult = httpRequest.request(url, { method: method, readTimeout: Constants.HTTP_READ_TIMEOUT, header: { 'Content-Type': ContentType.JSON }, connectTimeout: Constants.HTTP_READ_TIMEOUT, extraData: params }); let serverData = new ResponseResult(); // Processes the data and returns. return responseResult.then((value: http.HttpResponse) => { if (value.responseCode === Constants.HTTP_CODE_200) { // Obtains the returned data. let result = `${value.result}`; let resultJson: ResponseResult = JSON.parse(result); if (resultJson.code === Constants.SERVER_CODE_SUCCESS) { serverData.data = resultJson.data; } serverData.code = resultJson.code; serverData.msg = resultJson.msg; } else { serverData.msg = `${$r('app.string.http_error_message')}&${value.responseCode}`; } return serverData; }).catch(() => { serverData.msg = $r('app.string.http_error_message'); return serverData; }); } |
utils/Logger.ets
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 |
import { hilog } from '@kit.PerformanceAnalysisKit'; const LOGGER_PREFIX: string = 'News Release'; class Logger { private domain: number; private prefix: string; // format Indicates the log format string. private format: string = '%{public}s, %{public}s'; /** * constructor. * * @param prefix Identifies the log tag. * @param domain Indicates the service domain, which is a hexadecimal integer ranging from 0x0 to 0xFFFFF * @param args Indicates the log parameters. */ constructor(prefix: string = '', domain: number = 0xFF00) { this.prefix = prefix; this.domain = domain; } debug(...args: string[]): void { hilog.debug(this.domain, this.prefix, this.format, args); } info(...args: string[]): void { hilog.info(this.domain, this.prefix, this.format, args); } warn(...args: string[]): void { hilog.warn(this.domain, this.prefix, this.format, args); } error(...args: string[]): void { hilog.error(this.domain, this.prefix, this.format, args); } } export default new Logger(LOGGER_PREFIX); |
utils/ToastUtil.ets
|
1 2 3 4 5 6 7 8 9 10 |
import { promptAction } from '@kit.ArkUI'; import Constants from '../constants/Constants'; export function showToast(msg: string | Resource) { promptAction.showToast({ message: msg, duration: Constants.ANIMATION_DURATION }); } |
entryability
EntryAbility.ets
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 |
import { abilityAccessCtrl, AbilityConstant, UIAbility, Want } from '@kit.AbilityKit'; import { window } from '@kit.ArkUI'; import Logger from '../common/utils/Logger'; import { GlobalContext } from '../viewmodel/GlobalContext'; export default class EntryAbility extends UIAbility { onCreate(want: Want, launchParam: AbilityConstant.LaunchParam): void { Logger.info('testTag', '%{public}s', 'Ability onCreate'); GlobalContext.getContext().setObject('abilityWant', want); } onDestroy(): void | Promise<void> { Logger.info('testTag', '%{public}s', 'Ability onDestroy'); } onWindowStageCreate(windowStage: window.WindowStage): void { // Main window is created, set main page for this ability. Logger.info('testTag', '%{public}s', 'Ability onWindowStageCreate'); this.requestPermissions(); windowStage.loadContent('pages/MainPage', (err, data) => { if (err.code) { Logger.error('testTag', 'Failed to load the content. Cause: %{public}s', JSON.stringify(err) ?? ''); return; } Logger.info('testTag', 'Succeeded in loading the content. Data: %{public}s', JSON.stringify(data) ?? ''); }); } onWindowStageDestroy(): void { // Main window is destroyed, release UI related resources. Logger.info('testTag', '%{public}s', 'Ability onWindowStageDestroy'); } onForeground(): void { // Ability has brought to foreground. GlobalContext.getContext().setObject('isBackRouter', false); Logger.info('testTag', '%{public}s', 'Ability onForeground'); } onBackground(): void { // Ability has back to background. Logger.info('testTag', '%{public}s', 'Ability onBackground'); } private requestPermissions() { let atManager = abilityAccessCtrl.createAtManager(); atManager.requestPermissionsFromUser(this.context, ['ohos.permission.READ_MEDIA']) .then((data) => { Logger.info('testTag', '%{public}s', `request permission data result: ${data}`); }) .catch((err: Error) => { Logger.error('testTag', '%{public}s', `fail to request permission error:${err}`) }); } } |
pages
MainPage.ets
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 |
import Constants from '../common/constants/Constants'; import NewsList from '../view/NewsList'; import { router } from '@kit.ArkUI'; import NewsTypeViewModel from '../viewmodel/NewsTypeViewModel'; import NewsTypeBean from '../viewmodel/NewsTypeModel'; import { GlobalContext } from '../viewmodel/GlobalContext'; /** * MainPage */ @Entry @Component struct MainPage { @State tabBarArray: NewsTypeBean[] = NewsTypeViewModel.getDefaultTypeList(); @State currentIndex: number = 0; @Builder TabBuilder(index: number) { Column() { Text(this.tabBarArray[index].name) .height(Constants.FULL_PERCENT) .fontSize(this.currentIndex === index ? $r('app.float.bar_selected_font') : $r('app.float.bar_normal_font')) .fontWeight(this.currentIndex === index ? Constants.TYPE_FONT_WEIGHT : Constants.DESC_FONT_WEIGHT) .fontColor($r('app.color.title_color')) } .padding({ left: $r('app.float.normal_padding'), right: $r('app.float.normal_padding') }) .margin({ left: index === 0 ? $r('app.float.common_padding') : 0, right: index === this.tabBarArray.length - 1 ? $r('app.float.common_padding') : 0 }) } aboutToAppear() { // Request news category. NewsTypeViewModel.getNewsTypeList().then((typeList: NewsTypeBean[]) => { this.tabBarArray = typeList; }); } onPageShow() { if (GlobalContext.getContext().getObject('isBackRouter') === true) { GlobalContext.getContext().setObject('isBackRouter', false); let tempIndex = this.currentIndex; this.currentIndex = -1; this.currentIndex = tempIndex; } } build() { Stack() { Tabs() { ForEach(this.tabBarArray, (tabsItem: NewsTypeBean, index?: number) => { TabContent() { NewsList({ index, currentIndex: $currentIndex }) } .tabBar(this.TabBuilder(tabsItem.id)) }, (tabsItem: NewsTypeBean) => JSON.stringify(tabsItem)); } .barHeight($r('app.float.nav_height')) .height(Constants.FULL_PERCENT) .barMode(BarMode.Scrollable) .onChange((index: number) => { this.currentIndex = index; }) .vertical(false) Image($r('app.media.ic_add')) .width($r('app.float.btn_size')) .height($r('app.float.btn_size')) .margin({ bottom: $r('app.float.btn_margin'), right: $r('app.float.btn_margin') }) .onClick(() => { router.pushUrl({ url: 'pages/NewsAddPage' }); }) } .width(Constants.FULL_PERCENT) .height(Constants.FULL_PERCENT) .alignContent(Alignment.BottomEnd) .backgroundColor($r('app.color.listColor')) } } |
NewsAddPage.ets
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 |
import { fileSelect, fileUpload } from '../common/utils/FileUtil' import Logger from '../common/utils/Logger' import Constants from '../common/constants/Constants' import { showToast } from '../common/utils/ToastUtil' import ResponseResult from '../viewmodel/ResponseResult' import { NewsData, NewsFile } from '../viewmodel/NewsData' import NewsViewModel from '../viewmodel/NewsViewModel' import { GlobalContext } from '../viewmodel/GlobalContext' import { router } from '@kit.ArkUI' @Entry @Component struct NewsAddPage { title: string = '' content: string = '' @State imageUri: string = '' @State isUploading: boolean = false selectImage() { Logger.info('selectImage') fileSelect().then((uri: string) => { Logger.info(uri) this.imageUri = uri || '' }) } uploadNewsData() { if (this.title === '') { showToast($r('app.string.prompt_no_title')) return } if (this.content === '') { showToast($r('app.string.prompt_no_content')) return } if (this.imageUri === '') { showToast($r('app.string.prompt_no_file')) return } this.isUploading = true let serverData = fileUpload(getContext(this), this.imageUri) serverData.then((data: ResponseResult) => { let imageUrl = data.data let newsFile = new NewsFile() newsFile.id = 0 newsFile.url = imageUrl newsFile.type = 0 newsFile.newsId = 0 let newsData: NewsData = new NewsData() newsData.title = this.title newsData.content = this.content newsData.imagesUrl = [newsFile] NewsViewModel.uploadNews(newsData).then(() => { this.isUploading = false GlobalContext.getContext().setObject('isBackRouter', true) router.back() }).catch(() => { this.isUploading = false showToast($r('app.string.upload_error_message')) }) }).catch(() => { this.isUploading = false showToast($r('app.string.upload_error_message')) }) } build() { Stack() { Navigation() { Column() { Column() { TextInput({ placeholder: $r('app.string.title_default_text') }) .textInputExtend() .onChange((value: string) => { this.title = value; }) Divider() .dividerExtend() TextArea({ placeholder: $r('app.string.content_default_text') }) .textAreaExtend() .onChange((value: string) => { this.content = value }) Scroll() { Row() { Image(this.imageUri ? this.imageUri : $r('app.media.ic_add_pic')) .addImageExtend() .onClick(() => this.selectImage()) } .imageRowExtend() } .scrollExtend() } .topColumnExtend() Button($r('app.string.release_btn')) .releaseButtonExtend() .onClick(() => this.uploadNewsData()) } .mainColumnExtend() } .navigationExtend() } } } @Extend(Navigation) function navigationExtend() { .height(Constants.FULL_PERCENT) .title(Constants.RELEASE_TITLE) .titleMode(NavigationTitleMode.Mini) .backgroundColor($r('app.color.listColor')) } @Extend(Column) function mainColumnExtend() { .height(Constants.FULL_PERCENT) .justifyContent(FlexAlign.SpaceBetween) .padding({ left: $r('app.float.common_padding'), right: $r('app.float.common_padding'), bottom: $r('app.float.common_padding') }) } @Extend(Column) function topColumnExtend() { .borderRadius($r('app.float.edit_view_radius')) .backgroundColor(Color.White) .width(Constants.FULL_PERCENT) } @Extend(TextInput) function textInputExtend() { .fontSize($r('app.float.title_font')) .placeholderFont({ size: $r('app.float.title_font') }) .margin({ top: $r('app.float.common_padding') }) .fontColor($r('app.color.title_color')) .backgroundColor(Color.White) .width(Constants.FULL_PERCENT) .height($r('app.float.input_height')) } @Extend(Divider) function dividerExtend() { .opacity($r('app.float.divider_opacity')) .color($r('app.color.title_color')) .width(Constants.DIVIDER_WIDTH) } @Extend(TextArea) function textAreaExtend() { .placeholderFont({ size: $r('app.float.title_font') }) .fontColor($r('app.color.title_color')) .height($r('app.float.area_height')) .fontSize($r('app.float.title_font')) .margin({ top: $r('app.float.normal_padding') }) .backgroundColor(Color.White) } @Extend(Scroll) function scrollExtend() { .width(Constants.FULL_PERCENT) .align(Alignment.Start) .scrollable(ScrollDirection.Horizontal) } @Extend(Row) function imageRowExtend() { .padding($r('app.float.common_padding')) } @Extend(Image) function addImageExtend() { .width($r('app.float.img_size')) .height($r('app.float.img_size')) .objectFit(ImageFit.Cover) } @Extend(Button) function releaseButtonExtend() { .fontSize($r('app.float.title_font')) .height($r('app.float.release_btn_height')) .width($r('app.float.release_btn_width')) .margin({ bottom: $r('app.float.common_padding') }) } |
NewEditPage.ets
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 |
import { router } from '@kit.ArkUI'; import Constants from '../common/constants/Constants'; import { fileSelect, fileUpload } from '../common/utils/FileUtil'; import { NewsFile, NewsData } from '../viewmodel/NewsData'; import NewsViewModel from '../viewmodel/NewsViewModel'; import { showToast } from '../common/utils/ToastUtil'; import UploadingLayout from '../view/UploadingLayout'; import ResponseResult from '../viewmodel/ResponseResult'; import { GlobalContext } from '../viewmodel/GlobalContext'; /** * NewsEditPage. */ @Entry @Component struct NewsEditPage { title: string = ''; content: string = ''; @State imageUri: string = ''; @State isUploading: boolean = false; selectImage() { fileSelect().then((uri: string) => { this.imageUri = uri || ''; }); } uploadNewsData() { if (this.title === '') { showToast($r('app.string.prompt_no_title')); return; } if (this.content === '') { showToast($r('app.string.prompt_no_content')); return; } if (this.imageUri === '') { showToast($r('app.string.prompt_no_file')); return; } this.isUploading = true; let serverData = fileUpload(getContext(this), this.imageUri); serverData.then((data: ResponseResult) => { let imageUrl = data.data; let newsFile = new NewsFile(); newsFile.id = 0; newsFile.url = imageUrl; newsFile.type = 0; newsFile.newsId = 0; let newsData: NewsData = new NewsData(); newsData.title = this.title; newsData.content = this.content; newsData.imagesUrl = [newsFile]; NewsViewModel.uploadNews(newsData).then(() => { this.isUploading = false; GlobalContext.getContext().setObject('isBackRouter', true); router.back(); }).catch(() => { this.isUploading = false; showToast($r('app.string.upload_error_message')); }); }).catch(() => { this.isUploading = false; showToast($r('app.string.upload_error_message')); }); } build() { Stack() { Navigation() { Column() { Column() { TextInput({ placeholder: $r('app.string.title_default_text') }) .fontSize($r('app.float.title_font')) .placeholderFont({ size: $r('app.float.title_font') }) .margin({ top: $r('app.float.common_padding') }) .fontColor($r('app.color.title_color')) .backgroundColor(Color.White) .onChange((value: string) => { this.title = value; }) .width(Constants.FULL_PERCENT) .height($r('app.float.input_height')) Divider() .opacity($r('app.float.divider_opacity')) .color($r('app.color.title_color')) .width(Constants.DIVIDER_WIDTH) TextArea({ placeholder: $r('app.string.content_default_text') }) .placeholderFont({ size: $r('app.float.title_font') }) .fontColor($r('app.color.title_color')) .height($r('app.float.area_height')) .fontSize($r('app.float.title_font')) .margin({ top: $r('app.float.normal_padding') }) .backgroundColor(Color.White) .onChange((value: string) => { this.content = value; }) Scroll() { Row() { Image(this.imageUri ? this.imageUri : $r('app.media.ic_add_pic')) .width($r('app.float.img_size')) .height($r('app.float.img_size')) .objectFit(ImageFit.Cover) .onClick(() => this.selectImage()) } .padding($r('app.float.common_padding')) } .width(Constants.FULL_PERCENT) .scrollable(ScrollDirection.Horizontal) .align(Alignment.Start) } .borderRadius($r('app.float.edit_view_radius')) .backgroundColor(Color.White) .width(Constants.FULL_PERCENT) Button($r('app.string.release_btn')) .fontSize($r('app.float.title_font')) .height($r('app.float.release_btn_height')) .width($r('app.float.release_btn_width')) .margin({ bottom: $r('app.float.common_padding') }) .onClick(() => this.uploadNewsData()) } .padding({ left: $r('app.float.common_padding'), right: $r('app.float.common_padding'), bottom: $r('app.float.common_padding') }) .height(Constants.FULL_PERCENT) .justifyContent(FlexAlign.SpaceBetween) } .height(Constants.FULL_PERCENT) .title(Constants.RELEASE_TITLE) .titleMode(NavigationTitleMode.Mini) .backgroundColor($r('app.color.listColor')) if (this.isUploading) { UploadingLayout() } } } } |
view
FailureLayout.ets
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 |
import Constants from '../common/constants/Constants'; @Component export default struct FailureLayout { reloadAction = () => {}; build() { Column() { Image($r('app.media.ic_none')) .height($r('app.float.no_data_img_size')) .width($r('app.float.no_data_img_size')) Text($r('app.string.page_none_msg')) .opacity($r('app.float.no_data_opacity')) .fontSize($r('app.float.title_font')) .fontColor($r('app.color.title_color')) .margin({ top: $r('app.float.common_padding') }) Text($r('app.string.click_reload')) .opacity($r('app.float.no_data_opacity')) .fontSize($r('app.float.title_font')) .fontColor($r('app.color.color_index')) .padding($r('app.float.common_padding')) .onClick(this.reloadAction) } .width(Constants.FULL_PERCENT) .height(Constants.FULL_PERCENT) .justifyContent(FlexAlign.Center) } } |
LoadingLayout.ets
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 |
import Constants from '../common/constants/Constants'; @Component export default struct LoadingLayout { build() { Row() { Image($r('app.media.ic_pull_up_load')) .width($r('app.float.refresh_img_size')) .height($r('app.float.refresh_img_size')) Text($r('app.string.pull_up_load_text')) .margin({ left: $r('app.float.normal_padding') }) .fontSize($r('app.float.title_font')) .textAlign(TextAlign.Center) } .width(Constants.FULL_PERCENT) .height(Constants.CUSTOM_LAYOUT_HEIGHT) .justifyContent(FlexAlign.Center) } } |
LoadMoreLayout.ets
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 |
import RefreshLoadingClass from '../viewmodel/RefreshLoadingClass'; import Constants from '../common/constants/Constants'; /** * The load more layout component. */ @Component export default struct LoadMoreLayout { @ObjectLink loadMoreLayoutClass: RefreshLoadingClass; build() { Row() { Image(this.loadMoreLayoutClass.imageSrc) .width($r('app.float.refresh_img_size')) .height($r('app.float.refresh_img_size')) Text(this.loadMoreLayoutClass.textValue) .margin({ left: $r('app.float.normal_padding') }) .fontSize($r('app.float.title_font')) .textAlign(TextAlign.Center) } .clip(true) .width(Constants.FULL_PERCENT) .justifyContent(FlexAlign.Center) .height(this.loadMoreLayoutClass.heightValue) } } |
NewsItem.ets
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 |
import { NewsData, NewsFile } from '../viewmodel/NewsData'; import Constants from '../common/constants/Constants'; /** * The news list item component. */ @Component export default struct NewsItem { newsData: NewsData = new NewsData(); build() { Column() { Row() { Image($r('app.media.ic_news')) .height($r('app.float.title_font')) .aspectRatio(Constants.TYPE_ASPECT_RATIO) Text(this.newsData?.title) .fontSize($r('app.float.title_font')) .fontColor($r('app.color.title_color')) .layoutWeight(1) .maxLines(1) .lineHeight($r('app.float.title_line_height')) .fontFamily($r('app.string.harmony_hei_ti_medium')) .margin({ left: $r('app.float.normal_padding') }) .textOverflow({ overflow: TextOverflow.Ellipsis }) .fontWeight(Constants.TITLE_FONT_WEIGHT) } .alignItems(VerticalAlign.Center) .width(Constants.FULL_PERCENT) Text(this.newsData?.content) .fontSize($r('app.float.desc_font')) .fontFamily($r('app.string.harmony_hei_ti')) .opacity(Constants.DESC_OPACITY) .fontColor($r('app.color.title_color')) .lineHeight($r('app.float.desc_line_height')) .width(Constants.FULL_PERCENT) .maxLines(Constants.CONTENT_MAX_LINE) .fontWeight(Constants.DESC_FONT_WEIGHT) .textOverflow({ overflow: TextOverflow.Ellipsis }) Row({ space: Constants.ITEM_IMG_SPACE }) { ForEach((this.newsData.imagesUrl), (itemImg: NewsFile) => { Image(Constants.SERVER + itemImg?.url) .height(Constants.FULL_PERCENT) .aspectRatio(1) .objectFit(ImageFit.Cover) .borderRadius($r('app.float.item_img_border_radius')) }, (itemImg: NewsFile) => JSON.stringify(itemImg)) } .clip(true) .width(Constants.FULL_PERCENT) .height($r('app.float.item_img_size')) .margin({ top: $r('app.float.common_padding') }) Text(this.newsData?.source) .fontSize($r('app.float.source_font')) .fontColor($r('app.color.fontColor_text2')) .width(Constants.FULL_PERCENT) .margin({ top: $r('app.float.normal_padding') }) } .padding($r('app.float.common_padding')) } } |
NewsList.ets
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 |
import NewsItem from './NewsItem'; import LoadMoreLayout from './LoadMoreLayout'; import RefreshLayout from './RefreshLayout'; import { NewsData } from '../viewmodel/NewsData'; import Constants, { PageState } from '../common/constants/Constants'; import NewsViewModel from '../viewmodel/NewsViewModel'; import { showToast } from '../common/utils/ToastUtil'; import FailureLayout from './FailureLayout'; import LoadingLayout from './LoadingLayout'; import NoMoreLayout from './NoMoreLayout'; import RefreshListViewModel from '../viewmodel/RefreshListViewModel'; /** * The news list component. */ @Component export default struct NewsList { index: number = 0; @Watch('changeCategory') @Link currentIndex: number; @State refreshStore: RefreshListViewModel = new RefreshListViewModel(); changeCategory() { if (this.currentIndex !== this.index) { return; } this.refreshStore.currentPage = 1; NewsViewModel.getNewsList(this.refreshStore.currentPage, this.refreshStore.pageSize).then((data: NewsData[]) => { this.refreshStore.pageState = PageState.Success; if (data.length === this.refreshStore.pageSize) { this.refreshStore.currentPage++; this.refreshStore.hasMore = true; } else { this.refreshStore.hasMore = false; } this.refreshStore.newsData = data; }).catch((err: string | Resource) => { showToast(err); this.refreshStore.pageState = PageState.Fail; }); } aboutToAppear() { // Load data. this.changeCategory(); } reloadAction() { this.refreshStore.pageState = PageState.Loading; this.changeCategory(); } build() { Column() { if (this.refreshStore.pageState === PageState.Loading) { LoadingLayout() } else if (this.refreshStore.pageState === PageState.Success) { this.ListLayout() } else { FailureLayout({ reloadAction: () => { this.reloadAction(); } }) } } .width(Constants.FULL_PERCENT) .height(Constants.FULL_PERCENT) .justifyContent(FlexAlign.Center) .onTouch((event?: TouchEvent) => { if (event) { if (this.refreshStore.pageState === PageState.Success) { this.refreshStore.listTouchEvent(event); } } }) } @Builder ListLayout() { List({ space: Constants.LIST_SPACE }) { ListItem() { RefreshLayout({ refreshLoadingClass: this.refreshStore.refreshLayoutClass }) } ForEach(this.refreshStore.newsData, (item: NewsData) => { ListItem() { NewsItem({ newsData: item }) } .backgroundColor($r('app.color.white')) .borderRadius($r('app.float.item_border_radius')) }, (item: NewsData, index?: number) => JSON.stringify(item) + index) ListItem() { if (this.refreshStore.hasMore) { LoadMoreLayout({ loadMoreLayoutClass: this.refreshStore.loadingMoreClass }) } else { NoMoreLayout() } } } .width(Constants.FULL_PERCENT) .height(Constants.FULL_PERCENT) .padding({ left: $r('app.float.common_padding'), right: $r('app.float.common_padding') }) .backgroundColor($r('app.color.listColor')) .edgeEffect(EdgeEffect.None) .onScrollIndex((start: number, end: number) => { // Listen to the first index of the current list. this.refreshStore.startIndex = start; this.refreshStore.endIndex = end; }) } } |
NoMoreLayout.ets
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 |
/** * The No more data layout component. */ import Constants from '../common/constants/Constants'; @Component export default struct NoMoreLayout { build() { Row() { Text($r('app.string.prompt_message')) .margin({ left: $r('app.float.normal_padding') }) .fontSize($r('app.float.title_font')) .textAlign(TextAlign.Center) } .width(Constants.FULL_PERCENT) .justifyContent(FlexAlign.Center) .height(Constants.CUSTOM_LAYOUT_HEIGHT) } } |
RefreshLayout.ets
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 |
import RefreshLoadingClass from '../viewmodel/RefreshLoadingClass'; import Constants from '../common/constants/Constants'; /** * The refresh layout component. */ @Component export default struct RefreshLayout { @ObjectLink refreshLoadingClass: RefreshLoadingClass; build() { Row() { Image(this.refreshLoadingClass.imageSrc) .width($r('app.float.refresh_img_size')) .height($r('app.float.refresh_img_size')) Text(this.refreshLoadingClass.textValue) .margin({ left: $r('app.float.normal_padding') }) .fontSize($r('app.float.title_font')) .textAlign(TextAlign.Center) } .clip(true) .width(Constants.FULL_PERCENT) .justifyContent(FlexAlign.Center) .height(this.refreshLoadingClass.heightValue) } } |
UploadingLayout.ets
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 |
import Constants from '../common/constants/Constants'; @Component export default struct UploadingLayout { build() { Column() { Image($r('app.media.ic_pull_up_load')) .width($r('app.float.btn_size')) .height($r('app.float.btn_size')) Text($r('app.string.uploading_text')) .margin({ top: $r('app.float.common_padding') }) .fontSize($r('app.float.title_font')) .fontColor($r('app.color.title_color')) .textAlign(TextAlign.Center) } .width(Constants.FULL_PERCENT) .height(Constants.FULL_PERCENT) .justifyContent(FlexAlign.Center) } } |
viewmodel
GlobalContext.ets
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 |
export class GlobalContext { private constructor() { } private static instance: GlobalContext; private _objects = new Map<string, Object>(); public static getContext(): GlobalContext { if (!GlobalContext.instance) { GlobalContext.instance = new GlobalContext(); } return GlobalContext.instance; } getObject(value: string): Object | undefined { return this._objects.get(value); } setObject(key: string, objectClass: Object): void { this._objects.set(key, objectClass); } } |
NewsData.ets
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 |
/** * News list item info. */ export class NewsData { /** * News list item title. */ title: string = ''; /** * News list item content. */ content: string = ''; /** * News list item imagesUrl. */ imagesUrl: Array<NewsFile> = [new NewsFile()]; /** * News list item source. */ source: string = ''; } /** * News image list item info. */ export class NewsFile { /** * News image list item id. */ id: number = 0; /** * News image list item url. */ url: | Object | ArrayBuffer = ''; /** * News image list item type. */ type: number = 0; /** * News image list item newsId. */ newsId: number = 0; } |
NewsTypeModel.ets
|
1 2 3 4 5 6 7 8 9 10 |
export default class NewsTypeBean { id: number; name: ResourceStr; constructor(id: number, name: ResourceStr) { this.id = id; this.name = name; } } |
NewsTypeViewModel.ets
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 |
import NewsTypeBean from './NewsTypeModel' import ResponseResult from './ResponseResult'; import Constants from '../common/constants/Constants'; import { httpRequestGet } from '../common/utils/HttpUtil'; const DEFAULT_NEWS_TYPES: NewsTypeBean[] = [ new NewsTypeBean(0, $r('app.string.tab_all')), new NewsTypeBean(1, $r('app.string.tab_domestic')), new NewsTypeBean(2, $r('app.string.tab_international')), new NewsTypeBean(3, $r('app.string.tab_fun')), new NewsTypeBean(4, $r('app.string.tab_military')), new NewsTypeBean(5, $r('app.string.tab_sports')), new NewsTypeBean(6, $r('app.string.tab_science')) ]; class NewsTypeViewModel { /** * Get news type list from server. * * @return NewsTypeBean[] newsTypeList */ getNewsTypeList(): Promise<NewsTypeBean[]> { return new Promise((resolve: Function) => { let url = `${Constants.SERVER}/${Constants.GET_NEWS_TYPE}`; httpRequestGet(url).then((data: ResponseResult) => { if (data.code === Constants.SERVER_CODE_SUCCESS) { resolve(data.data); } else { resolve(DEFAULT_NEWS_TYPES); } }).catch(() => { resolve(DEFAULT_NEWS_TYPES); }); }); } /** * Get default news type list. * * @return NewsTypeBean[] newsTypeList */ getDefaultTypeList(): NewsTypeBean[] { return DEFAULT_NEWS_TYPES; } } let newsTypeViewModel = new NewsTypeViewModel(); export default newsTypeViewModel as NewsTypeViewModel; |
NewsViewModel.ets
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 |
import { NewsData } from './NewsData'; import ResponseResult from './ResponseResult'; import Constants from '../common/constants/Constants'; import { httpRequestGet, httpRequestPost } from '../common/utils/HttpUtil'; import Logger from '../common/utils/Logger'; class NewsViewModel { /** * Get news type list from server. * * @return NewsData[] newsDataList */ getNewsList(currentPage: number, pageSize: number): Promise<NewsData[]> { return new Promise(async (resolve: Function, reject: Function) => { let url = `${Constants.SERVER}/${Constants.GET_NEWS_LIST}`; url += '?currentPage=' + currentPage + '&pageSize=' + pageSize; httpRequestGet(url).then((data: ResponseResult) => { if (data.code === Constants.SERVER_CODE_SUCCESS) { resolve(data.data); } else { Logger.error('getNewsList failed', JSON.stringify(data)); reject($r('app.string.page_none_msg')); } }).catch((err: Error) => { Logger.error('getNewsList failed', JSON.stringify(err)); reject($r('app.string.http_error_message')); }); }); } /** * Upload news data. * * @param newsData * @returns NewsData[] newsDataList */ uploadNews(newsData: NewsData): Promise<NewsData[]> { return new Promise((resolve: Function, reject: Function) => { let url = `${Constants.SERVER}/${Constants.UPLOAD_NEWS}`; httpRequestPost(url, newsData).then((result: ResponseResult) => { if (result && result.code === Constants.SERVER_CODE_SUCCESS) { resolve(result.data); } else { reject($r('app.string.upload_error_message')); } }).catch((err: Error) => { Logger.error('uploadNews failed', JSON.stringify(err)); reject($r('app.string.upload_error_message')); }); }); } } let newsViewModel = new NewsViewModel(); export default newsViewModel as NewsViewModel; |
RefreshListViewModel.ets
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199 200 201 202 203 204 205 206 207 208 209 210 |
import { promptAction } from '@kit.ArkUI'; import Constants, { RefreshState, RefreshConstant, PageState } from '../common/constants/Constants'; import NewsViewModel from './NewsViewModel'; import { NewsData } from './NewsData'; import RefreshLoadingClass from './RefreshLoadingClass'; @Observed export default class RefreshListViewModel { private downY = 0; private lastMoveY = 0; private isRefreshing: boolean = false; private isCanRefresh = false; private isPullRefreshOperation = false; private isLoading: boolean = false; private isCanLoadMore = false; public startIndex = 0; public endIndex = 0; public newsData: Array<NewsData> = []; public currentPage: number = 1; public pageSize: number = 4; public offsetY: number = 0; public hasMore: boolean = true; public refreshLayoutClass: RefreshLoadingClass = new RefreshLoadingClass($r('app.media.ic_pull_down_refresh'), $r('app.string.pull_down_refresh_text'), 0); public loadingMoreClass: RefreshLoadingClass = new RefreshLoadingClass($r('app.media.ic_pull_up_load'), $r('app.string.pull_up_load_text'), 0); public pageState: number = PageState.Loading; listTouchEvent(event: TouchEvent) { switch (event.type) { case TouchType.Down: this.downY = event.touches[0].y; this.lastMoveY = event.touches[0].y; break; case TouchType.Move: if (this.isRefreshing || this.isLoading) { return; } let isDownPull = event.touches[0].y - this.lastMoveY > 0; if ((isDownPull || this.isPullRefreshOperation) && !this.isCanLoadMore) { // Touch move pull refresh. this.touchMovePullRefresh(event); } else { // Touch move load more. this.touchMoveLoadMore(event); } this.lastMoveY = event.touches[0].y; break; case TouchType.Cancel: break; case TouchType.Up: if (this.isRefreshing || this.isLoading) { return; } if (this.isPullRefreshOperation) { // Touch up pull refresh. this.touchUpPullRefresh(); } else { // Touch up load more. this.touchUpLoadMore(); } break; default: break; } } touchMovePullRefresh(event: TouchEvent) { if (this.startIndex === 0) { this.isPullRefreshOperation = true; let height = vp2px(Constants.CUSTOM_LAYOUT_HEIGHT); this.offsetY = event.touches[0].y - this.downY; // Check offsetY to Refresh. if (this.offsetY >= height) { this.pullRefreshState(RefreshState.Release); this.offsetY = height + this.offsetY * Constants.Y_OFF_SET_COEFFICIENT; } else { this.pullRefreshState(RefreshState.DropDown); } if (this.offsetY < 0) { this.offsetY = 0; this.isPullRefreshOperation = false; } } } touchUpPullRefresh() { if (this.isCanRefresh) { this.offsetY = vp2px(Constants.CUSTOM_LAYOUT_HEIGHT); this.pullRefreshState(RefreshState.Refreshing); this.currentPage = 1; setTimeout(() => { NewsViewModel.getNewsList(this.currentPage, this.pageSize).then((data: NewsData[]) => { if (data.length === this.pageSize) { this.currentPage++; this.hasMore = true; } else { this.hasMore = false; } this.newsData = data; this.closeRefresh(true); }).catch((errMsg: string | Resource) => { promptAction.showToast({ message: errMsg }); this.closeRefresh(false); }) }, Constants.DELAY_TIME); } else { this.closeRefresh(false); } } pullRefreshState(state: number) { switch (state) { case RefreshState.DropDown: this.isCanRefresh = false; this.isRefreshing = false; this.refreshLayoutClass = new RefreshLoadingClass($r('app.media.ic_pull_down_refresh'), $r('app.string.pull_down_refresh_text'), Constants.CUSTOM_LAYOUT_HEIGHT) break; case RefreshState.Release: this.refreshLayoutClass.imageSrc = $r('app.media.ic_pull_up_refresh'); this.refreshLayoutClass.textValue = $r('app.string.release_refresh_text'); this.isCanRefresh = true; this.isRefreshing = false; break; case RefreshState.Refreshing: this.offsetY = vp2px(this.refreshLayoutClass.heightValue); this.refreshLayoutClass.imageSrc = $r('app.media.ic_pull_up_load'); this.refreshLayoutClass.textValue = $r('app.string.refreshing_text'); this.isCanRefresh = true; this.isRefreshing = true; break; case RefreshState.Success: this.refreshLayoutClass.imageSrc = $r('app.media.ic_succeed_refresh'); this.refreshLayoutClass.textValue = $r('app.string.refresh_success_text'); this.isCanRefresh = true; this.isRefreshing = true; break; case RefreshState.Fail: this.refreshLayoutClass.imageSrc = $r('app.media.ic_fail_refresh'); this.refreshLayoutClass.textValue = $r('app.string.refresh_fail_text'); this.isCanRefresh = true; this.isRefreshing = true; break; default: break; } } closeRefresh(isRefreshSuccess: boolean) { setTimeout(() => { let delay = RefreshConstant.DELAY_PULL_DOWN_REFRESH; if (this.isCanRefresh) { this.pullRefreshState(isRefreshSuccess ? RefreshState.Success : RefreshState.Fail); delay = RefreshConstant.DELAY_SHRINK_ANIMATION_TIME; } animateTo({ duration: RefreshConstant.CLOSE_PULL_DOWN_REFRESH_TIME, delay: delay, onFinish: () => { this.pullRefreshState(RefreshState.DropDown); this.refreshLayoutClass.heightValue = 0; this.isPullRefreshOperation = false; } }, () => { this.offsetY = 0; }); }, this.isCanRefresh ? Constants.DELAY_ANIMATION_DURATION : 0); } touchMoveLoadMore(event: TouchEvent) { if (this.endIndex >= this.newsData.length - 1) { this.offsetY = event.touches[0].y - this.downY; if (Math.abs(this.offsetY) > vp2px(Constants.CUSTOM_LAYOUT_HEIGHT) / 2) { this.isCanLoadMore = true; this.loadingMoreClass.heightValue = Constants.CUSTOM_LAYOUT_HEIGHT; this.offsetY = -vp2px(Constants.CUSTOM_LAYOUT_HEIGHT) + this.offsetY * Constants.Y_OFF_SET_COEFFICIENT; } } } touchUpLoadMore() { if (this.isCanLoadMore && this.hasMore) { this.isLoading = true; setTimeout(() => { NewsViewModel.getNewsList(this.currentPage, this.pageSize).then((data: NewsData[]) => { if (data.length === this.pageSize) { this.currentPage++; this.hasMore = true; } else { this.hasMore = false; } this.newsData = this.newsData.concat(data); }).catch((errMsg: string | Resource) => { promptAction.showToast({ message: errMsg }); }) this.closeLoadMore(); }, Constants.DELAY_TIME); } else { this.closeLoadMore(); } } closeLoadMore() { this.isCanLoadMore = false; this.isLoading = false; this.loadingMoreClass.heightValue = 0; } } |
RefreshLoadingClass.ets
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 |
/** * Custom refresh load layout data. */ @Observed export default class RefreshLoadingClass { /** * Custom refresh load layout imageSrc. */ imageSrc: Resource; /** * Custom refresh load layout textValue. */ textValue: Resource; /** * Custom refresh load layout heightValue. */ heightValue: number; constructor(imageSrc: Resource, textValue: Resource, heightValue: number) { this.imageSrc = imageSrc; this.textValue = textValue; this.heightValue = heightValue; } } |
ResponseResult.ets
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 |
/** * Data returned by the network request. */ export default class ResponseResult { /** * Code returned by the network request: success, fail. */ code: string; /** * Message returned by the network request. */ msg: string | Resource; /** * Data returned by the network request. */ data: string | Object | ArrayBuffer; constructor() { this.code = ''; this.msg = ''; this.data = ''; } } |
配置
module.json5
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 |
{ "module": { "name": "entry", "type": "entry", "description": "$string:module_desc", "mainElement": "EntryAbility", "deviceTypes": [ "phone" ], "deliveryWithInstall": true, "installationFree": false, "pages": "$profile:main_pages", "abilities": [ { "name": "EntryAbility", "srcEntry": "./ets/entryability/EntryAbility.ets", "description": "$string:EntryAbility_desc", "icon": "$media:icon", "label": "$string:EntryAbility_label", "startWindowIcon": "$media:icon", "startWindowBackground": "$color:start_window_background", "exported": true, "skills": [ { "entities": [ "entity.system.home" ], "actions": [ "action.system.home" ] } ] } ], "requestPermissions": [ { "name": "ohos.permission.INTERNET", "reason": "$string:reason", "usedScene": { "abilities": [ "EntryAbility" ], "when": "inuse" } } ] } } |
下载源码
官网地址
往HarmonyOS模拟器相册添加图片
HarmonyOS第一课07:案例-HTTPS请求过程
HarmonyOS第一课07:案例-新闻数据加载
HarmonyOS第一课07:HTTP数据请求
HarmonyOS第一课06:设置组件导航
关联章节
- HarmonyOS第一课05:案例
- HarmonyOS第一课05:应用架构设计基础——MVVM模式
- HarmonyOS第一课05:应用架构设计基础——三层架构
- HarmonyOS第一课06:ArkWeb页面适配
- HarmonyOS第一课06:通过结构化数据构建页面
说明:本章代码基于HarmonyOS第一课06:通过结构化数据构建页面代码
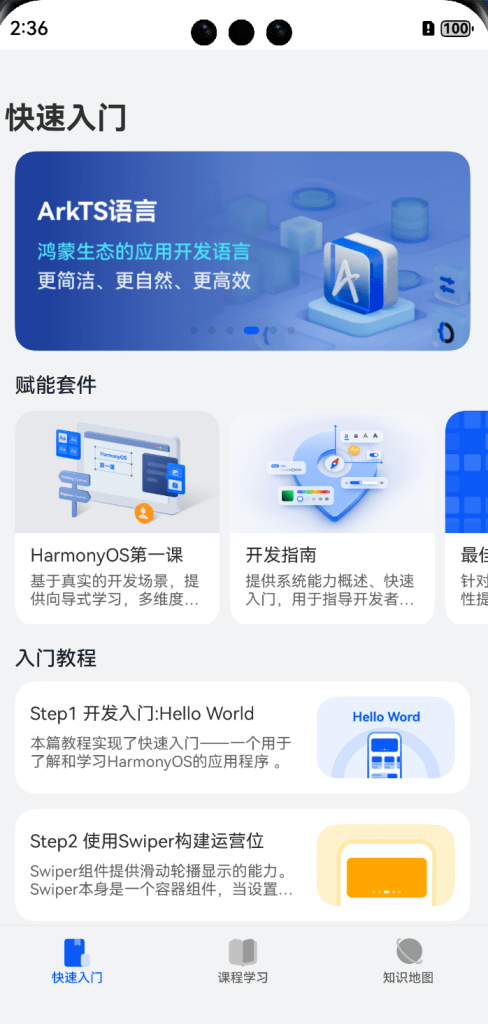
页面效果
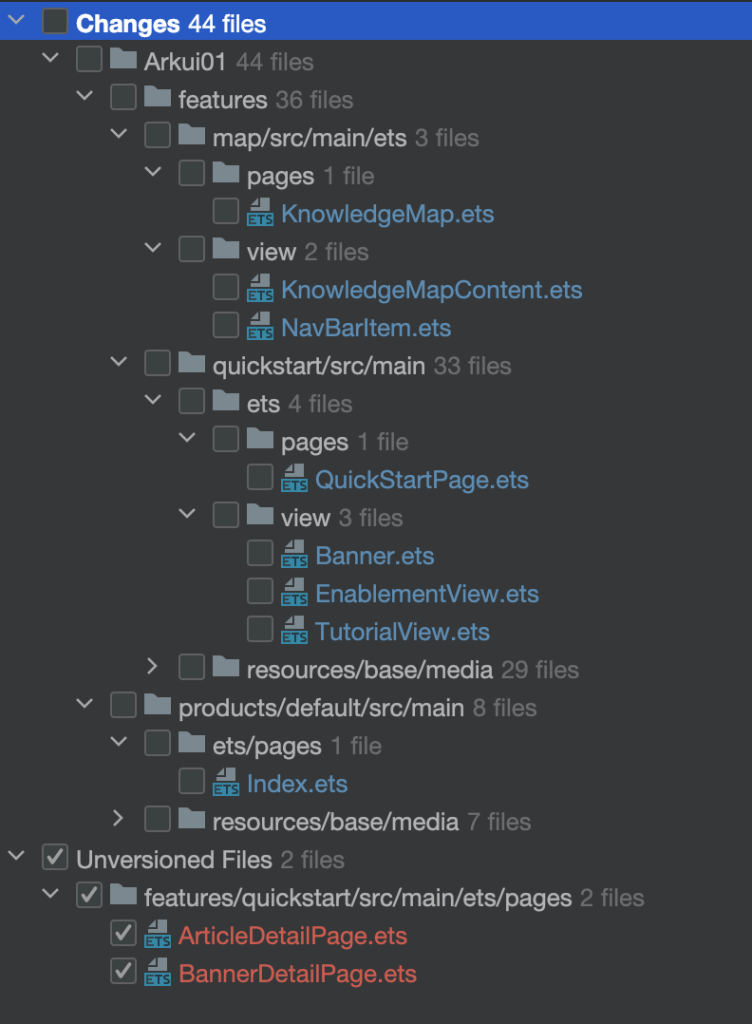
文件变动
代码
default
pages/Index.ets
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 |
import { QuickStartPage } from '@ohos/quickstart' import { CourseLearning } from '@ohos/learning' import { KnowledgeMap } from '@ohos/map' @Entry @Component struct Index { @State currentIndex: number = 0 private tabsController: TabsController = new TabsController() @Builder tabBarBuilder(title: string, targetIndex: number, selectedIcon: Resource, unselectIcon: Resource) { Column() { Image(this.currentIndex === targetIndex ? selectedIcon : unselectIcon) .width(24) .height(24) Text(title) .fontFamily('HarmonyHeiTi-Medium') .fontSize(10) .fontColor(this.currentIndex === targetIndex ? '#0A59F7' : 'rgba(0,0,0,0.6)') .textAlign(TextAlign.Center) .lineHeight(14) .fontWeight(500) } .width('100%') .height('100%') .justifyContent(FlexAlign.Center) .alignItems(HorizontalAlign.Center) .onClick(() => { this.currentIndex = targetIndex this.tabsController.changeIndex(targetIndex) }) } build() { Tabs({ barPosition: BarPosition.End, controller: this.tabsController }) { TabContent() { QuickStartPage() } .tabBar(this.tabBarBuilder('快速入门', 0, $r('app.media.ic_01_on'), $r('app.media.ic_01_off'))) TabContent() { CourseLearning() } .tabBar(this.tabBarBuilder('课程学习', 1, $r('app.media.ic_02_on'), $r('app.media.ic_02_off'))) TabContent() { KnowledgeMap() } .tabBar(this.tabBarBuilder('知识地图', 2, $r('app.media.ic_03_on'), $r('app.media.ic_03_off'))) } .scrollable(false) .vertical(false) .divider({ strokeWidth: 0.5, color: '#0D182431' }) .backgroundColor('#F1F3F5') .padding({ top: 36, bottom: 28 }) } } |
map
pages/KnowledgeMap.ets
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 |
import { NavBarItemType, NavBarItem } from '../view/NavBarItem' import { KnowledgeMapContent, Section } from '../view/KnowledgeMapContent' import { BusinessError } from '@kit.BasicServicesKit' import { util } from '@kit.ArkTS' @Component export struct KnowledgeMap { @State navBarList: NavBarItemType[] = [ { order: '01', title: '准备与学习' }, { order: '02', title: '构建应用' }, { order: '03', title: '应用测试' }, { order: '04', title: '上架' }, { order: '05', title: '运营增长' }, { order: '06', title: '商业变现' }, { order: '07', title: '更多' } ] @State sections: Section[] = [] @Provide('knowledgeMapPageStack') knowledgeMapPageStack: NavPathStack = new NavPathStack() @State currentNavBarIndex: number = -1 @Builder PageMap(name: string) { if (name === 'KnowledgeMapContent') { KnowledgeMapContent({ section: this.sections[this.currentNavBarIndex] }) } } private getSections() { try { getContext(this).resourceManager.getRawFileContent("MapData.json", (error: BusinessError, value: Uint8Array) => { const textDecoder = util.TextDecoder.create('utf-8') const res = textDecoder.decodeWithStream(value, { stream: false }) this.sections = JSON.parse(res) }) } catch (error) { console.error(`callback getRawFileContent failed, error is ${JSON.stringify(error)}`) } } aboutToAppear(): void { this.getSections() } build() { Navigation(this.knowledgeMapPageStack) { Scroll() { Column() { Text('知识地图') .fontFamily('HarmonyHeiTi-Bold') .fontSize(24) .fontColor(Color.Black) .textAlign(TextAlign.Start) .lineHeight(33) .fontWeight(700) .width('100%') Image($r('app.media.knowledge_map_banner')) .width('100%') .borderRadius(16) .margin({ top: 19, bottom: 8 }) Text('通过循序渐进的学习路径,无经验和有经验的开发者都可以轻松掌握ArkTS语言声明式开发范式,体验更简洁、更友好的HarmonyOS应用开发旅程。') .fontFamily('HarmonyHeiti') .fontSize(14) .fontColor('rgba(0, 0, 0, 0.6)') .fontWeight(400) .textAlign(TextAlign.Start) List({ space: 12 }) { ForEach(this.navBarList, (item: NavBarItemType, index: number) => { ListItem() { NavBarItem({ navBarItem: item, currentNavBarIndex: this.currentNavBarIndex }) } .width('100%') }, (item: NavBarItemType): string => item.title) } .width('100%') .margin({ top: 24 }) } .padding({ top: 12, right: 16, bottom: 12, left: 16 }) .backgroundColor("#F1F3F5") } .backgroundColor('#F1F3F5') .align(Alignment.TopStart) .constraintSize({ minHeight: '100%' }) .edgeEffect(EdgeEffect.Spring) } .hideTitleBar(true) .navDestination(this.PageMap) .mode(NavigationMode.Stack) } } |
view/KnowledgeMapContent.ets
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 |
interface KnowledgeBaseItem { type: string, title: string } interface Material { subtitle: string, knowledgeBase: KnowledgeBaseItem[] } export interface Section { title: string, brief: string, materials: Material[] } const TypeMapIcon: Record<string, string> = { '指南': 'app.media.ic_guide', '准备': 'app.media.ic_prepare', '学习与获取证书': 'app.media.ic_medals', '视频教程': 'app.media.ic_video' } @Component export struct KnowledgeMapContent { @Prop section: Section @Builder KnowledgeBlockLine(knowledgeBaseItem: KnowledgeBaseItem) { Row() { Image($r(TypeMapIcon[knowledgeBaseItem.type])) .width(20) .height(20) Column() { Text(knowledgeBaseItem.title) .fontFamily('HarmonyHeiTi-Medium') .fontSize(16) .fontWeight(500) Text(knowledgeBaseItem.type) .fontFamily('HarmonyHeiTi') .fontSize(14) .fontWeight(400) } .alignItems(HorizontalAlign.Start) .margin({ left: 18 }) Blank() Image($r('app.media.ic_arrow')) .width(12) .height(24) } .width('100%') .height(64) .alignItems(VerticalAlign.Center) } @Builder KnowledgeBlock(material: Material) { Column() { Text(material.subtitle) .fontFamily('HarmonyHeiTi-Medium') .fontSize(14) .fontWeight(500) .margin({ bottom: 8 }) List({ space: 12 }) { ForEach(material.knowledgeBase, (item: KnowledgeBaseItem, index: number) => { ListItem() { this.KnowledgeBlockLine(item) } }, (item: KnowledgeBaseItem, index: number) => item.title) } .backgroundColor(Color.White) .borderRadius(16) .padding({ left: 12, right: 12 }) .divider({ strokeWidth: 0.5, startMargin: 38, endMargin: 0, color: '#F2F2F2' }) } .width('100%') .margin({ top: 28 }) .alignItems(HorizontalAlign.Start) } build() { NavDestination() { Scroll() { Column() { Text(this.section.title) .fontFamily('HarmonyHeiTi-Bold') .fontSize(20) .fontWeight(700) .fontColor(Color.Black) Text(this.section.brief) .fontFamily('HarmonyHeiTi') .fontSize(12) .fontColor('rgba(0, 0, 0, 0.6)') .textAlign(TextAlign.JUSTIFY) .fontWeight(400) .margin({ top: 12 }) ForEach(this.section.materials, (material: Material) => { this.KnowledgeBlock(material) }, (material: Material, index: number) => material.subtitle) } .alignItems(HorizontalAlign.Start) .padding({ top: 12, left: 16, bottom: 12, right: 16 }) .backgroundColor('#F1F3F5') .width('100%') } .align(Alignment.TopStart) .constraintSize({ minHeight: '100%' }) .edgeEffect(EdgeEffect.Spring) .scrollable(ScrollDirection.Vertical) .scrollBar(BarState.Auto) .backgroundColor('#F1F3F5') } .hideTitleBar(true) } } |
view/NavBarItem.ets
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 |
export interface NavBarItemType { order: string title: string } @Component export struct NavBarItem { @Prop navBarItem: NavBarItemType @Consume('knowledgeMapPageStack') knowledgeMapPageStack: NavPathStack @Link currentNavBarIndex: number build() { Row() { Text(this.navBarItem.order) .margin({ right: 6 }) .fontFamily('HarmonyHeiti-Bold') .fontSize(21) .fontColor('#182431') .textAlign(TextAlign.Start) .lineHeight(22) .fontWeight(700) Text(this.navBarItem.title) .fontFamily('HarmonyHeiti-Medium') .fontSize(16) .fontColor('#182431') .lineHeight(22) .fontWeight(500) Blank() Image($r('app.media.ic_arrow')) .width(12) .height(24) } .width('100%') .height(48) .borderRadius(16) .alignItems(VerticalAlign.Center) .padding({ left: 12, right: 12 }) .backgroundColor( this.currentNavBarIndex === Number(this.navBarItem.order) - 1 ? '#1A0A59F7' : Color.Transparent ) .onClick(() => { const index = Number(this.navBarItem.order) - 1 this.currentNavBarIndex = index this.knowledgeMapPageStack.replacePath({ name: 'KnowledgeMapContent' }) }) } } |
quickstart
pages/QuickStartPage.ets
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 |
import { TutorialView } from '../view/TutorialView' import { Banner } from '../view/Banner' import { EnablementView } from '../view/EnablementView' import { ArticleClass } from '../model/ArticleClass' import { BannerClass } from '../model/BannerClass' import { ArticleDetailPage } from './ArticleDetailPage' import { BannerDetailPage } from './BannerDetailPage' @Component export struct QuickStartPage { @State message: string = '快速入门' @Provide('articlePathStack') articlePathStack: NavPathStack = new NavPathStack() @Builder quickStartRouter(name: string, param?: ArticleClass | BannerClass) { if (name === 'articleDetail') { ArticleDetailPage() } else if (name === 'bannerDetailPage') { BannerDetailPage() } } build() { Navigation(this.articlePathStack) { Column() { Text(this.message) .fontFamily('HarmonyHeiTi-Bold') .fontSize(24) .fontWeight(700) .lineHeight(33) .width('100%') .textAlign(TextAlign.Start) .margin({ left: 16 }) Scroll() { Column() { Banner() EnablementView() TutorialView() } } .layoutWeight(1) .scrollBar(BarState.Off) .align(Alignment.TopStart) } .height('100%') .width('100%') .backgroundColor('#F1F3F5') } .navDestination(this.quickStartRouter) .hideTitleBar(true) .mode(NavigationMode.Stack) } } |
pages/ArticleDetailPage.ets
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 |
import { ArticleClass } from '../model/ArticleClass' import { webview } from '@kit.ArkWeb' @Preview @Component export struct ArticleDetailPage { @State articleDetail: ArticleClass | null = null @Consume('articlePathStack') articlePathStack: NavPathStack aboutToAppear(): void { this.articleDetail = this.articlePathStack.getParamByName('articleDetail')[0] as ArticleClass } build() { NavDestination() { Column() { Row() { Row() { Image($r('app.media.ic_back')) .width(40) .height(40) .onClick(() => { this.articlePathStack.pop() }) Row() { Text(this.articleDetail?.title) .fontFamily('HarmonyHeiTi-Bold') .fontSize(20) .textAlign(TextAlign.Center) .textOverflow({ overflow: TextOverflow.Ellipsis }) .maxLines(1) .fontWeight(700) .margin({ left: 8 }) } } .width('80%') } .justifyContent(FlexAlign.SpaceBetween) .width('100%') .height(56) WebComponent({ articleDetail: this.articleDetail }) } .padding({ left: 16, right: 16 }) .width('100%') .width('100%') .height('100%') .justifyContent(FlexAlign.SpaceBetween) } .hideTitleBar(true) } } @Component struct WebComponent { @Prop articleDetail: ArticleClass | null private webviewController: webview.WebviewController = new webview.WebviewController() build() { Column() { Web({ src: this.articleDetail?.webUrl, controller: this.webviewController }) .darkMode(WebDarkMode.Auto) .domStorageAccess(true) .zoomAccess(true) .fileAccess(true) .mixedMode(MixedMode.All) .cacheMode(CacheMode.None) .javaScriptAccess(true) .width('100%') .layoutWeight(1) } } } |
pages/BannerDetailPage.ets
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 |
import { BannerClass } from '../model/BannerClass' import { webview } from '@kit.ArkWeb' @Component export struct BannerDetailPage { @State bannerClass: BannerClass | null = null controller: webview.WebviewController = new webview.WebviewController() @Consume('articlePathStack') articlePathStack: NavPathStack aboutToAppear(): void { this.bannerClass = this.articlePathStack.getParamByName('bannerDetailPage')[0] as BannerClass } build() { NavDestination() { Column() { Web({ src: this.bannerClass?.url, controller: this.controller }) .darkMode(WebDarkMode.Auto) .domStorageAccess(true) .zoomAccess(true) .fileAccess(true) .mixedMode(MixedMode.All) .javaScriptAccess(true) .width('100%') .layoutWeight(1) } } .width('100%') .height('100%') } } |
view/Banner.ets
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 |
import { BannerClass } from '../model/BannerClass' import { bufferToString } from '../util/BufferUtil' @Preview @Component export struct Banner { @State bannerList: BannerClass[] = [] @Consume('articlePathStack') articlePathStack: NavPathStack getBannerDataFromJSON() { getContext(this).resourceManager.getRawFileContent('BannerData.json').then(value => { // 获取buffer内容 // let buffer: ArrayBufferLike = value.buffer // 转换为字符串 // let res: string = bufferToString(buffer) // 解析为数据结构 // this.bannerList = JSON.parse(res) as BannerClass[] // 简写 this.bannerList = JSON.parse(bufferToString(value.buffer)) as BannerClass[] }) } aboutToAppear(): void { this.getBannerDataFromJSON() } build() { Swiper() { ForEach(this.bannerList, (item: BannerClass, index: number) => { Image($r(item.imageSrc)) .objectFit(ImageFit.Contain) .width('100%') .padding({ top: 11, left: 16, right: 16 }) .borderRadius(16) .onClick(() => { this.articlePathStack.pushPathByName('bannerDetailPage', item) }) }, (item: BannerClass, index: number) => item.id) } .autoPlay(true) .loop(true) .indicator( new DotIndicator() .color('#1a000000') .selectedColor('#0A59F7') ) } } |
view/EnablementView.ets
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 |
import { ArticleClass } from '../model/ArticleClass' import { bufferToString } from '../util/BufferUtil' @Component struct EnablementItem { @Prop enablementItem: ArticleClass build() { Column() { Image($r(this.enablementItem.imageSrc)) .width('100%') .objectFit(ImageFit.Cover) .height(96) .borderRadius({ topLeft: 16, topRight: 16 }) Text(this.enablementItem.title) .height(19) .width('100%') .fontSize(14) .textAlign(TextAlign.Start) .textOverflow({ overflow: TextOverflow.Ellipsis }) .maxLines(1) .fontWeight(400) .padding({ left: 12, right: 12 }) .margin({ top: 8 }) Text(this.enablementItem.brief) .height(32) .width('100%') .fontSize(12) .textAlign(TextAlign.Start) .textOverflow({ overflow: TextOverflow.Ellipsis }) .maxLines(2) .fontWeight(400) .fontColor('rgba(0, 0, 0, 0.6)') .padding({ left: 12, right: 12 }) .margin({ top: 2 }) } .width(160) .height(169) .borderRadius(16) .backgroundColor(Color.White) } } @Preview @Component export struct EnablementView { @State enablementList: Array<ArticleClass> = [] @Consume('articlePathStack') articlePathStack: NavPathStack aboutToAppear(): void { this.getEnablementDataFromJSON() } getEnablementDataFromJSON() { getContext(this).resourceManager.getRawFileContent('EnablementData.json').then(value => { this.enablementList = JSON.parse(bufferToString(value.buffer)) as ArticleClass[] }) } build() { Column() { Text('赋能套件') .width('100%') .fontColor('#182431') .fontSize(16) .fontWeight(500) .fontFamily('HarmonyHeiTi-medium') .textAlign(TextAlign.Start) .padding({ left: 16 }) .margin({ bottom: 8.5 }) Grid() { ForEach(this.enablementList, (item: ArticleClass) => { GridItem() { EnablementItem({ enablementItem: item }) .onClick(() => { this.articlePathStack.pushPathByName('articleDetail', item) }) } }, (item: ArticleClass) => item.id) } .rowsTemplate('1fr') .columnsGap(8) .scrollBar(BarState.Off) .height(169) .padding({ top: 2, left: 16, right: 16 }) } .width('100%') .margin({ top: 18 }) } } |
view/TutorialView.ets
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 |
import { ArticleClass } from '../model/ArticleClass' import { bufferToString } from '../util/BufferUtil' @Component struct TutorialItem { @Prop tutorialItem: ArticleClass build() { Row() { Column() { Text(this.tutorialItem.title) .height(19) .width('100%') .fontSize(14) .textAlign(TextAlign.Start) .textOverflow({ overflow: TextOverflow.Ellipsis }) .maxLines(1) .fontWeight(400) .margin({ top: 4 }) Text(this.tutorialItem.brief) .height(32) .width('100%') .fontSize(12) .textAlign(TextAlign.Start) .textOverflow({ overflow: TextOverflow.Ellipsis }) .maxLines(2) .fontWeight(400) .fontColor('rgba(0, 0, 0, 0.6)') .margin({ top: 5 }) } .height('100%') .layoutWeight(1) .alignItems(HorizontalAlign.Start) .margin({ right: 12 }) Image($r(this.tutorialItem.imageSrc)) .height(64) .width(108) .objectFit(ImageFit.Cover) .borderRadius(16) } .width('100%') .height(88) .borderRadius(16) .backgroundColor(Color.White) .padding(12) .alignItems(VerticalAlign.Top) } } @Preview @Component export struct TutorialView { @State tutorialList: Array<ArticleClass> = [] @Consume('articlePathStack') articlePathStack: NavPathStack aboutToAppear(): void { this.getTutorialDataFromJSON() } getTutorialDataFromJSON() { getContext(this).resourceManager.getRawFileContent('TutorialData.json').then(value => { this.tutorialList = JSON.parse(bufferToString(value.buffer)) as ArticleClass[] }) } build() { Column() { Text('入门教程') .fontColor('#182431') .fontSize(16) .fontWeight(500) .fontFamily('HarmonyHeiTi-medium') .textAlign(TextAlign.Start) .padding({ left: 16 }) .margin({ bottom: 8.5 }) List({ space: 12 }) { ForEach(this.tutorialList, (item: ArticleClass) => { ListItem() { TutorialItem({ tutorialItem: item }) .onClick(() => { this.articlePathStack.pushPathByName('articleDetail', item) }) } }, (item: ArticleClass) => item.id) } .scrollBar(BarState.Off) .padding({ left: 16, right: 16 }) } .width('100%') .margin({ top: 18 }) .alignItems(HorizontalAlign.Start) } } |
下载源码
官网地址
https://developer.huawei.com/consumer/cn/training/course/slightMooc/C101717497640610394