complex方法是Python内置函数,用于创建复数。复数由实部和虚部组成,形式为 $ a + bi $,其中 $ a $ 是实部,$ b $ 是虚部。
下面是如何使用 complex 方法的详细说明和示例:
一、基本用法
complex 方法可以接受两个参数,分别是实部和虚部。如果只提供一个参数,则虚部默认值为0。
|
1 2 3 4 5 |
z1 = complex(1, 2) # 创建复数 1 + 2i z2 = complex(3) # 创建复数 3 + 0i print("复数 z1:", z1) print("复数 z2:", z2) |
二、从字符串创建复数
complex 方法还可以接受一个字符串参数,该字符串应该表示一个复数。如果字符串格式不正确,则会引发 ValueError。
|
1 2 3 4 5 |
z3 = complex("1+2j") # 创建复数 1 + 2i z4 = complex("3-4j") # 创建复数 3 - 4i print("复数 z3:", z3) print("复数 z4:", z4) |
三、属性和方法
创建复数后,可以使用 .real 和 .imag 属性来访问复数的实部和虚部,还可以使用 conjugate 方法来获取共轭复数。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 |
z = complex(1, -2) # 实部 real_part = z.real print("实部:", real_part) # 虚部 imag_part = z.imag print("虚部:", imag_part) # 共轭复数 z_conjugate = z.conjugate() print("共轭复数:", z_conjugate) |
四、复数运算
使用 complex 方法创建复数后,可以进行各种复数运算,如加、减、乘、除等。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 |
z1 = complex(1, 2) z2 = complex(3, -4) # 加法 z_sum = z1 + z2 print("复数相加:", z_sum) # 输出 (4-2j) # 减法 z_diff = z1 - z2 print("复数相减:", z_diff) # 输出 (-2+6j) # 乘法 z_prod = z1 * z2 print("复数相乘:", z_prod) # 输出 (11+2j) # 除法 z_div = z1 / z2 print("复数相除:", z_div) # 输出 (-0.2+0.4j) |
这些示例展示了如何使用 complex 方法来创建和操作复数。复数在许多数学和工程应用中都非常有用,了解如何在Python中处理复数是非常重要的。
五、复数运算原理
复数运算遵循特定的数学规则,考虑实部和虚部的操作。以下是复数运算的基本原理,包括加法、减法、乘法和除法:
复数的表示
- 复数 $ z = a + bi $,其中 $ a $ 是实部,$ b $ 是虚部,$ i $ 是虚数单位,满足 $ i^2 = -1 $。
加法和减法
- 将对应的实部和虚部分别相加或相减。
- 设 $ z_1 = a_1 + b_1i $ 和 $ z_2 = a_2 + b_2i $:
- 加法: $ z_1 + z_2 = (a_1 + a_2) + (b_1 + b_2)i $
- 减法: $ z_1 – z_2 = (a_1 – a_2) + (b_1 – b_2)i $
乘法
- 使用分配律展开,并利用 $ i^2 = -1 $。
- 设 $ z_1 = a_1 + b_1i $ 和 $ z_2 = a_2 + b_2i $:
- 乘法: $ z_1 \cdot z_2 = (a_1 + b_1i)(a_2 + b_2i) = a_1a_2 + a_1b_2i + b_1a_2i + b_1b_2i^2 $
- 简化: $ z_1 \cdot z_2 = (a_1a_2 – b_1b_2) + (a_1b_2 + b_1a_2)i $
除法
- 乘以共轭复数,以消除分母中的虚部。
- 设 $ z_1 = a_1 + b_1i $ 和 $ z_2 = a_2 + b_2i $,并令 $ \overline{z_2} = a_2 – b_2i $(共轭复数):
- 除法: $ \frac{z_1}{z_2} = \frac{(a_1 + b_1i)(a_2 – b_2i)}{(a_2 + b_2i)(a_2 – b_2i)} $
- 分母: $ (a_2 + b_2i)(a_2 – b_2i) = a_2^2 + b_2^2 $
- 分子: $ (a_1 + b_1i)(a_2 – b_2i) = a_1a_2 – a_1b_2i + b_1a_2i – b_1b_2i^2 = a_1a_2 + b_1b_2 + (b_1a_2 – a_1b_2)i $
- 最终结果: $ \frac{z_1}{z_2} = \frac{a_1a_2 + b_1b_2}{a_2^2 + b_2^2} + \frac{b_1a_2 – a_1b_2}{a_2^2 + b_2^2}i $
让我们通过Python示例代码和打印结果来展示这些运算原理:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 |
# 加法和减法 z1 = complex(1, 2) # 1 + 2i z2 = complex(3, -4) # 3 - 4i z_sum = z1 + z2 z_diff = z1 - z2 print("复数相加:", z_sum) # (4-2j) print("复数相减:", z_diff) # (-2+6j) # 乘法 z_prod = z1 * z2 print("复数相乘:", z_prod) # (11+2j) # 除法 z_div = z1 / z2 print("复数相除:", z_div) # (-0.2+0.4j) |
打印结果:
|
1 2 3 4 |
复数相加: (4-2j) 复数相减: (-2+6j) 复数相乘: (11+2j) 复数相除: (-0.2+0.4j) |
通过这些示例,你可以看到复数的加法、减法、乘法和除法的具体运算过程和结果。理解这些运算有助于在实际应用中更好地处理复数。
复数可以通过向量的方式在二维平面上表示。通常称为复平面或阿尔冈图平面,其中横轴代表实部,纵轴代表虚部。
六、向量坐标解释复数运算
加法和减法(向量)
在复平面上,复数的加法和减法可以通过向量的起点和终点来表示。
- 加法:两个复数的加法就是将对应向量的起点和终点相连的结果。
- 减法:两个复数的减法就是将一个向量的起点移到另一个向量的终点,结果是从起点到终点的新向量。
例如:
- $ z_1 = 1 + 2i $ 对应向量 $(1, 2)$
- $ z_2 = 3 – 4i $ 对应向量 $(3, -4)$
加法: $ z_1 + z_2 = (1 + 3) + (2 – 4)i = 4 – 2i $
减法: $ z_1 – z_2 = (1 – 3) + (2 – (-4))i = -2 + 6i $
乘法(向量)
复数乘法涉及向量的旋转和缩放:
- 模长(向量长度):两个复数的模长相乘。
- 角度(向量与实轴的夹角):两个复数的角度相加。
例如:
- $ z_1 = 1 + 2i $ 的模长是 $ \sqrt{1^2 + 2^2} = \sqrt{5} $
- $ z_2 = 3 – 4i $ 的模长是 $ \sqrt{3^2 + (-4)^2} = 5 $
乘法: $ z_1 \cdot z_2 = \sqrt{5} \cdot 5 = 5\sqrt{5} $
除法(向量)
复数除法也涉及模长和角度:
- 模长:两个复数的模长相除。
- 角度:被除数的角度减去除数的角度。
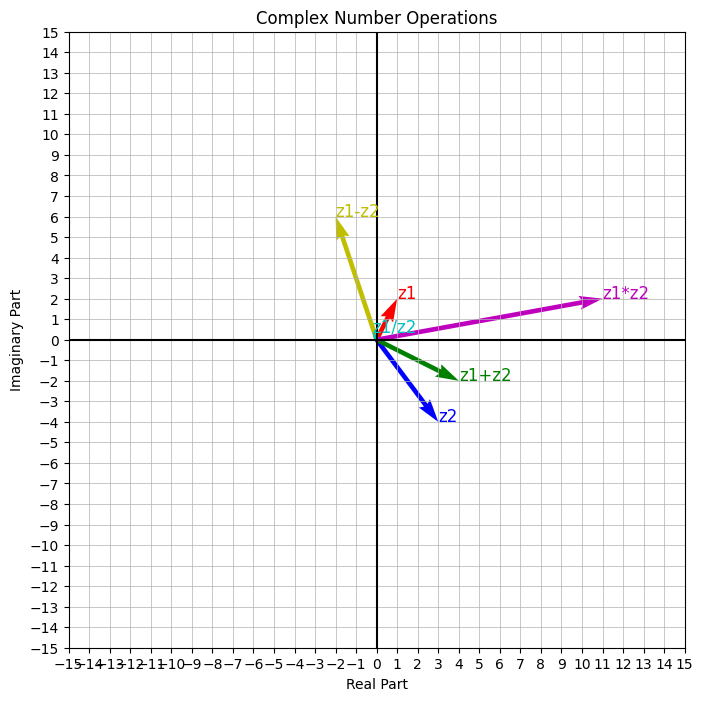
七、详细图例演示
我们可以使用Python的matplotlib库来绘制这些运算的图例:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 |
import matplotlib.pyplot as plt import numpy as np def plot_complex_operations(): # 定义复数 z1 = complex(1, 2) z2 = complex(3, -4) # 定义向量 vectors = np.array([[0, 0, z1.real, z1.imag], [0, 0, z2.real, z2.imag], [0, 0, (z1+z2).real, (z1+z2).imag], [0, 0, (z1-z2).real, (z1-z2).imag], [0, 0, (z1*z2).real, (z1*z2).imag], [0, 0, (z1/z2).real, (z1/z2).imag]]) # 创建图表 fig, ax = plt.subplots(figsize=(8, 8)) ax.quiver(vectors[:,0], vectors[:,1], vectors[:,2], vectors[:,3], angles='xy', scale_units='xy', scale=1, color=['r','b','g','y','m','c']) # 标记向量 ax.text(z1.real, z1.imag, 'z1', fontsize=12, color='r') ax.text(z2.real, z2.imag, 'z2', fontsize=12, color='b') ax.text((z1+z2).real, (z1+z2).imag, 'z1+z2', fontsize=12, color='g') ax.text((z1-z2).real, (z1-z2).imag, 'z1-z2', fontsize=12, color='y') ax.text((z1*z2).real, (z1*z2).imag, 'z1*z2', fontsize=12, color='m') ax.text((z1/z2).real, (z1/z2).imag, 'z1/z2', fontsize=12, color='c') # 设置轴和网格 ax.axhline(y=0, color='k') ax.axvline(x=0, color='k') # 设置网格线宽度为1,并增加网格线密度 ax.grid(True, which='both', linewidth=0.5) # 设置主刻度 ax.xaxis.set_major_locator(plt.MultipleLocator(1)) ax.yaxis.set_major_locator(plt.MultipleLocator(1)) # 设置次刻度 ax.xaxis.set_minor_locator(plt.MultipleLocator(1)) ax.yaxis.set_minor_locator(plt.MultipleLocator(1)) ax.set_aspect('equal') plt.xlabel('Real Part') plt.ylabel('Imaginary Part') plt.title('Complex Number Operations') plt.xlim(-15, 15) plt.ylim(-15, 15) plt.show() plot_complex_operations() |
八、使用场景和作用
复数及其运算在许多领域中有广泛的应用:
- 电路分析:在交流电路中,电压和电流常用复数表示,方便计算。
- 信号处理:复数用于表示和分析信号的频率和相位信息。
- 量子力学:复数用于描述量子态和概率幅。
- 控制系统:复数用于描述系统的特征根和稳定性。
- 计算机图形学:复数用于图像处理和变换,例如傅里叶变换。
这些示例和图例展示了复数的基本运算及其在数学和工程中的重要应用。理解复数运算有助于在这些领域进行有效的分析和计算。

